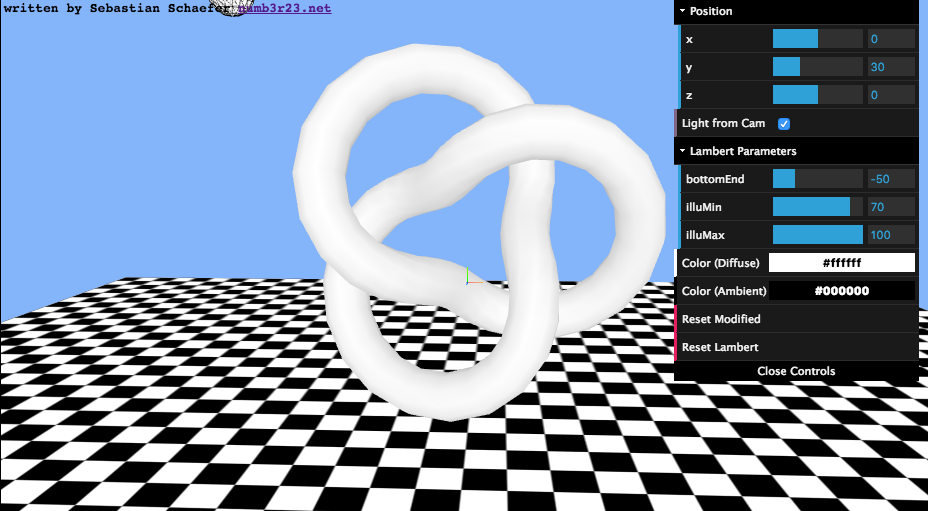
Analytic, function-based distance fields are great for drawing things procedurally in the shader. As long as you can combine a few function and model the distance right you can simply create sharp-looking geometrical objects – even complex combinations are possible. The following is also true for texture-based distance fields (sdf fonts), but I’ve decided to give distance functions the space they deserve.

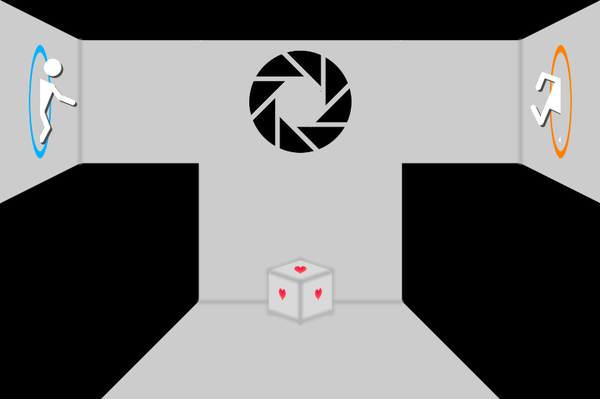
2D portal, composed of 2D distance field functions

One of the great aspects of these functions is that they can be evaluated for every pixel independent of a target resolution and can thus be used to create a proper, anti-aliased images. If you set it up right.

Instead of the usual circle example where the distance is simple the distance(coordinate, center) and create a diamond pattern:

Distance Field Diamond

float dst = dot(abs(coord-center), vec2(1.0));

Using a radius as a step/threshold we can very easily create “diamonds” in the size we like:

Diamond Step Function

vec3 color = vec3(1.0 - step(radius, dst));

So far so good. what’s missing is now the antialiasing part of it all – the step function creates a hard edge. Enter smoothstep, a function that performs a hermite interpolation between two values:

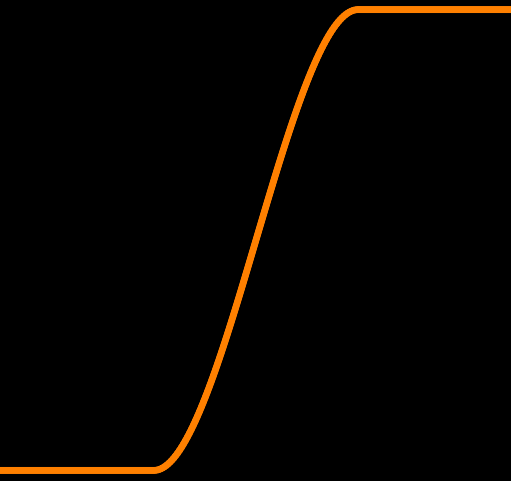
y = smoothstep(0.3, 0.7, x)

If both values are the same, it boils down to a step. What we now want is to “blend” the diamond into the background, ideally on the border pixels (and therefor not wider than 1 pixel). If we had such a value, let’s call it “aaf” (= anti-aliasing-factor), we could smoothly fade-out the diamond into the background:

Diamond Smoothstep

vec3 color = vec3(1.0 - smoothstep(radius - aaf, radius, dst));

Luckily most OpenGL implementations have the three functions dFdx, dFdy and fwidth:

• dFdx calculates the change of the parameter along the viewport’s x-axis
• dFdy calculates the change of the parameter along the viewport’s y-axis
• fwidth is effectively abs(dFdx) + abs(dFdy) and gives you the positive change in both directions

The functions are present in >= GLSL 110 on desktop or >= GLSL ES 3.0. For es pre-GLSL 3.0 there’s an extension GL_OES_standard_derivatives that allows to enable the usage:

#extension GL_OES_standard_derivatives : enable

But how does it connect together? What we need is the effective change of the distance field per pixel so we can identify a single pixel for the distance field. Since we need this for both axis we can do this:

float aaf = fwidth(dst);

fwidth evaluates the change of the distance field, the value stored in the variable dst, for the current pixel – relative to it’s screen tile. The size of that change determines how wide our smoothstep interpolation needs to be set up in order to fade out the pattern on a per pixel level. The antialiasing fade can be used in numerous ways:

• store it in the alpha-channel and do regular alpha-blending
• use it to blend between two colors with a mix
• use it to blend in a single pattern element

The whole shader boils down to this:

float dst = dot(abs(coord-center), vec2(1.0));
float aaf = fwidth(dst);
float alpha = smoothstep(radius - aaf, radius, dst);
vec4 color = vec4(colDiamond, alpha);

Selected remarks:

• fwidth is not free. in fact, it’s rather expensive. Try not to call it too much!
• it’s great if you can sum up all distances so that you can arrive at a single dst-value so you only call fwidth once.
• give fwidth the variable you want to smoothstep. Not the underlying coordinate – that’s a completely different change and would lead to a wrong-sized filter
• length(fwidth(coord)) is “ok”, but not great if you look closely. Depending e.g. on the distortion/transformation applied to the coordinates to derive the distance value it might look very odd.

Enjoy!